Can Development Of Liposomes for Drug Delivery Be Made Easy Using Mathematical Optimization Techniques?

This post is going to be a little different from others. It is something I have had in mind for quite some time regarding drug delivery, and would like to discuss with readers who are well versed with drug delivery to understand whether or not this is a worthwhile direction of research. In its content, this post is going to be a little more technical than my other posts. But I’ll do my best to minimize the use of specialized technical terms, and explain the meaning of those that I do end up using, to keep the post as readable as possible for folks from all areas of expertise. Let’s start with the meaning of drug delivery.

Drug Delivery

As the name suggests, drug delivery is the process of successfully delivering a drug to its target in the body, which can be some particular type of cell, some molecule, or come pathogenic microbe. Hence, drug delivery involves development of formulations, technologies and systems for achieving this objective. And its harder than it sounds. Once a drug enters the human body, it encounters multiple barriers on its path to its target.

If you take a drug orally, it needs to stay intact in the intensely acidic environment of the stomach, then somehow cross the intestinal lining to enter the blood stream. The blood vessels supplying the digestive system take all the contents absorbed from the intestines straight to the liver, where the nutrients are sent onward in the blood stream to the rest of the body, excess nutrients are stored in the liver to be released later, and toxins are converted into harmless molecules that are excreted through the kidneys.

So, once in blood stream, the drug goes to the liver. The liver usually sees the drug as a toxin, and hence attempts to degrade it and send the residue to kidneys for excretion. Drug molecules that escape degradation must then circulate throughout the body through the blood stream, until they reach their target organ. Once they reach the target organ, the drug molecules must often enter the cell to bind their target molecule, if the target molecule happens to be inside cells, instead of on their surface or outside. This presents yet another barrier.

In addition to all these, the drugs acting on the brain encounter the blood brain barrier, which is an additional layer of cells covering the blood vessels supplying to the brain. All these barriers make drug delivery a not so easy task to accomplish. There are various methods to make drug delivery easier. For example, if you inject the drug directly into the blood stream instead making the patient take it orally, it would bypass the digestive system and the intestinal lining barriers.

If you inject the drug in a blood vessel that doesn’t go to the liver but directly to the target organ, the drug would bypass the liver as well, and directly go to the target organ instead of circulating throughout the body first. But researchers are now trying to come up with methods that deliver the drug specifically to the target cells, and not to any other type of cell. This should not only make drug delivery easier, thereby reducing the dose of drug required, but also reduce the side effects by preventing drug from entering the wrong type of cells. One way to do this is to deliver the drug through liposomes.

Liposomes

Liposomes are microscopic, spherical objects, with diameters in nanometers. Their surface is made of a lipid bilayer, which is the same structure of which the membrane of cells in our body is made. Liposomes are hollow from inside, which enables them to carry various molecules inside them. And the surface of liposomes can be fitted with various molecules for different purposes. For example, an antibody that binds to a specific protein on the surface of a specific type of cell, can be attached to a liposome’s surface. This would enable the liposome to recognize that specific type of cell.

Then a molecule that makes the liposome surface, or membrane, fuse with the membrane of that cell, can also be attached to the liposome. This would enable the liposome to release its inner contents into the cell. The fusion of liposome’s membrane with the cell membrane is possible because, as I said before, both the liposome membrane and cell membrane are made of the same chemical structure- the lipid bilayer. Chemically speaking, this fusion of liposome with cell is somewhat similar to fusion of two oil drops floating in water.

And then there are molecules you attach on the liposome’s surface to make it difficult to be recognized and destroyed by the body’s immune system, and hence increase the liposome’s chances of reaching its target cell intact and delivering its contents into it.

Liposomes can be used to deliver various types of molecular cargoes to target cells. They can be used to deliver DNA into a target cell as a part of gene therapy, or they can be used to deliver a conventional drug molecule into the target cell to treat some other disorder. The video below gives a brief introduction to liposomes. But before I elaborate more on liposomes, I will use a simple example to explain what mathematical optimization techniques are.

Optimization Techniques

You are a furniture dealer, and you deal in two items- tables and chairs. A chair costs ₹ 500 and a table costs ₹ 2,500. You have ₹ 50,000 to invest, and have storage space for 60 pieces. You can make a profit of ₹ 250 from the sale of one table and a profit of ₹ 75 from the sale of one chair. Obviously, you would like to know how many tables and how many chairs you should buy from your 50,000 bucks, in order to maximize your profits. In what combination you buy tables and chairs affects your profit.

Such a problem is called an optimization problem. Optimization problems seek to maximize a desired quantity (like profit), or minimize it (like cost or consumption of resources). One of the simplest and most basic types of optimization problems is linear programming optimization problem. The problem of furniture dealer above is also a linear programming optimization problem.

In the above example, suppose you buy only tables and no chairs. With your ₹ 50,000, you can buy 50,000 / 2,500 = 20 tables. In this case, your profit will be 250 x 20 = Rs. 5000. Similarly, suppose you buy only chairs and no tables. With your ₹ 50,000, you can buy 50,000 / 500 = 100 chairs. But as you have storage space for just 60 units, you can buy a maximum of just 60 chairs. Buying 60 chairs will give you a profit of 75 x 60 = ₹ 4,500. Suppose you buy 10 tables and 50 chairs, which reaches the maximum storage limit of 60 units. In this case, your profit will be 10 x 250 + 50 x 75 = ₹ 6250. There are numerous buying options.

So what’s the best investment strategy for your 50,000? The optimum number of tables and chairs to buy to maximize profit? To find this out, we need to formulate the problem mathematically. Suppose the number of tables bought is x and the number of chairs bought is y. Obviously, these two numbers cannot be less than zero. Mathematically, we can write this fact as,

x ≥ 0 ; y ≥ 0

A table costs 2,500 and a chair costs 500. And the maximum amount you can invest is 50,000. Mathematically we can write this as,

2500x + 500y ≤ 50000

Or, 5x + y ≤ 100

The maximum storage space you have is for 60 units. Mathematically you can write this as,

x + y ≤ 60

Suppose the profit you make is Z. Your objective is to buy tables and chairs in a combination that maximizes profit. Hence,

Z = 250x + 70y needs to be maximized. This linear equation which has to be maximized is called objective function. And the constraints this maximization is subjected to are,

x ≥ 0 ; y ≥ 0

x + y ≤ 60

5x + y ≤ 100

If you plot these constraints on a graph, it will look like the figure below.

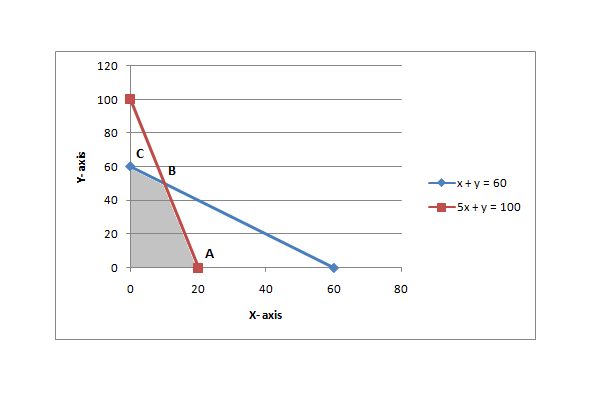
The shaded region in the graph shows the investment options options that you have. Each point in the shaded region is a unique combination of tables and chairs that you can buy with a maximum investment of ₹ 50,000 and maximum storage capacity of 60 units. The x coordinate of each point represents the number of tables in that combination, and y coordinate represents the number of chairs.

The points outside the shaded region also show the different combinations of tables and chairs that you can buy. But they are not subject to the constraints that the number of tables plus chairs must not exceed 60, and the money spent buying them must not exceed ₹ 50,000. The points below the x axis and on the left side of y axis also represent various combinations of tables and chairs. But the numbers of tables and chairs in them are negative, or less than zero, which s a physical impossibility. In other words, these points are not just free from constraints x + y ≤ 60 and 5x + y = 100, but are also free from the constraints x ≥ 0 and y ≥ 0.

Hence, it is only the points inside the shaded region that are subject to all the constraints you have, and hence these alone are the points representing viable buying choices for you. Now, how do you find out which of these points within the shaded region represents the combination of tables and chairs that maximizes your profit? For this, we must remember two theorems that are central to linear programming.

Theorem 1: The optimal solution to the objective function lies at one of the corner points of the feasible region. in other words, the maximum or minimum value of the quantity that we want to maximize or minimize (profit Z in our case) lies at one of the corner points of the polygon formed by the shaded region.

Theorem 2: If the feasible region is bounded, then both the maximum and minimum values of the objective function lie on the corner points of the feasible region. In other words, if the shaded region is not infinite, but bounded on all sides by constraints (as in our case), then both the maximum and minimum values of the quantity we want to optimize (profit Z in our case) lie on the corner points of the polygon formed by the shaded region.

Now, in our case, the corner points formed by the shaded region are O (with x = 0 and y = 0), A (with x = 20 and y = 0), B (with x = 10 and y = 50) and C (with x = 0 and y = 60). When you enter these values for x and y in the equation for profit Z = 250x + 70y, you will find that the values of Z for different values of x and y are ₹ 0 for point o (obviously), ₹ 5000 for point A, ₹ 6250 for point B and ₹ 4500 for point C. This means that you will make maximum profit (₹ 6250) if you procure 10 tables and 50 chairs (x and y coordinates of B).

Using Optimization Techniques In Development Of Liposomes For Drug Delivery

Now that we have seen how linear programming can be used to optimize a desired quantity, like maximizing profit or minimizing cost, let’s look at a hypothetical situation in which we could use the same approach in development of liposome based drug delivery vehicles. Suppose a liposome contains a drug meant to target a specific molecule inside a specific type of cell. It has two different molecules attached on its surface. Let these two molecules be x and y respectively. Molecule x is the antibody that recognizes the type of cell in which the liposome has to inject the drug. And molecule y leads to the injection of the drug into the cell through membrane fusion.

Now, my assumption is that the efficiency with which the liposome recognizes the right type of cell increases as we increase the number of x molecules on its surface. This is because higher numbers will increase the chances that molecule x will find and bind its target molecule on the surface of the cell (It can distinguish this cell type from other types of cells because the target molecule it binds to is found only on the surface of this cell type and not on any other type of cells). Similarly, the probability of membrane fusion and injection of drug into the cell will increase with increase in the number of y molecules.

Now here is the problem. The liposome is a sphere with a finite surface area. And molecules x and y also occupy specific, finite areas. This means that only a limited number of x and y molecules can be incorporated on the liposome’s surface. There would be a maximum number of molecules that the liposome’s surface can accommodate (just like the maximum storage capacity of 60 units in the furniture problem we saw above). Once you reach this maximum limit, further increasing the number of x molecules will decrease the number of y molecules and vice versa. But the liposome needs both x and y molecules for successful drug delivery.

The question then is, at what numbers of x and y molecules will the efficiency of the liposome as a drug delivery vehicle be maximum? We are looking at an optimization problem here. Let’s look at the constraints. Obviously, the numbers of x and y molecules can’t be less than zero. Hence two of the constraints are,

x ≥ 0 ; y ≥ 0

Suppose the surface area of the liposome is 100 square units (just a rough estimation). Then the constraint restricting the maximum number of x and y molecules on the liposome’s surface would be,

x + y ≤ 100

If we plot these three constraints on a graph, we will get the figure below.

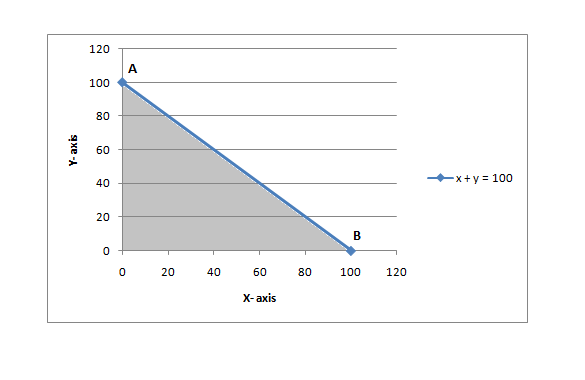
Recall that according to the theorems I mentioned above, the maximum and minimum values of the quantity of interest are found at the corner points of the shaded region. But it is here that I start finding it hard to proceed further with mathematical formulation of this problem. And it is from this point onward, that I hope to discuss with you readers, on how to proceed.

The shaded region in the graph we have above is a triangle, and hence it has only three corners. One of the three corners is the origin, and hence denotes zero number of both x and y molecules. Then there is the point on X axis, denoting maximum number of x molecules, which is 100, with zero y molecules. And then there is the point on Y axis, denoting maximum number of y molecules, which is 100, with zero x molecules.

Obviously, none of these combinations represent the optimum solution. Because the liposome needs to carry both x and y molecules on its surface to successfully deliver the drug to the right type of cells. So what’s missing here? Its a third constraint. Remember that in the furniture problem above, we had one constraint representing the maximum storage capacity of 60 units, and another constraint representing the maximum investment capacity of ₹ 50,000.

In the case of our liposome problem, we have introduced the constraint of maximum number of x or y molecules that can be incorporated on the liposome’s surface. This constraint is analogous to the constraint of maximum storage capacity in the furniture problem. But we haven’t introduced any constraint in liposome problem, which is similar to the constraint of maximum investment capacity in the furniture problem.

So, my question is, what kind of additional constraint is needed in this problem, that I am missing? A constraint whose line would intersect the line of the constraint representing maximum number of x or y molecules, so that the intersecting point can show a combination of x and y molecules that would optimize the ability of the liposome to deliver its drug to the right type of cells? It must be remembered that the affinity of the molecules x and y for their receptors, and not just their numbers on the liposome, will also determine the liposome’s efficiency. Does the missing constraint have something to do with that aspect?

Another question I have is, is this a relevant direction of research? Do you think this approach could help in development of more efficient drug delivery vehicles? Or are the current methods of maximizing efficiency of drug delivery vehicles good, fast and cheap enough?

There are also more sophisticated optimization techniques than linear programming. Could they be more useful in development of efficient drug delivery vehicles? After all, in our example we have assumed that the liposome will have only two types of molecules on its surface. But in reality, more types of molecules may need to be incorporated. Also, do let me know if you are aware of any similar method that has been applied in the past for development of drug delivery vehicles.